A mathematics major must have a love of the abstract and deduction. Mathematics majors take classes such as calculus, linear algebra, and analysis to broaden their knowledge of the objects and ideas used by mathematicians daily. They build extensive problem-solving skills and develop techniques to approach the world of ideas in a critical and logical manner. As the “language of science,” mathematics greatly aids our understanding of questions posed in physics, biology, chemistry, and computer science, as well as economics, sociology, and other fields, and many day-to-day issues.
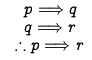 At its heart, modern mathematics uses the rules of logic and rigor to deduce results from basic defined concepts. The rigor of mathematics makes its methods suitable in some fundamental way to solving problems. One can infer complex conclusions from simple assumptions by being creative and applying the rules of logic. Developing strong logical acuity helps one think critically, and supports an open-minded approach to any problem he or she might come across.
At its heart, modern mathematics uses the rules of logic and rigor to deduce results from basic defined concepts. The rigor of mathematics makes its methods suitable in some fundamental way to solving problems. One can infer complex conclusions from simple assumptions by being creative and applying the rules of logic. Developing strong logical acuity helps one think critically, and supports an open-minded approach to any problem he or she might come across.
There is a common misconception that mathematics is a rigid science in which everything has been discovered, and that everything is dry and lifeless in the field. Nothing could be further from the truth – there are a great many unsolved problems to tackle in all fields of math! These unanswered questions benefit from fresh, creative minds coming at them with ingenious ideas and novel approaches.
Some people are amazed at just how well mathematics works, especially with respect to the sciences. Physicist Eugene Wigner addressed this point in his 1960 essay “The Unreasonable Effectiveness of Mathematics in the Natural Sciences”. The essay gives non-scientists a flavor of how a physicist might think about mathematics’ place in science and the world in general. See our page on writings by mathematicians about mathematics for more.
 There are numerous subjects to explore in both pure and applied mathematics. Pure mathematics is the study of “mathematics for mathematics’ sake”, plumbing further into the depths of abstraction. Applications of mathematics are sometimes not readily apparent. Results in group theory from the 1700’s now help give us a theory of symmetries used in physics and chemistry, and centuries-old number theory results about prime numbers are now of utmost importance in the computer programming that encrypts our credit card transactions and other secure data online. When these discoveries were made, they were profound results, but with no technological application in sight.
There are numerous subjects to explore in both pure and applied mathematics. Pure mathematics is the study of “mathematics for mathematics’ sake”, plumbing further into the depths of abstraction. Applications of mathematics are sometimes not readily apparent. Results in group theory from the 1700’s now help give us a theory of symmetries used in physics and chemistry, and centuries-old number theory results about prime numbers are now of utmost importance in the computer programming that encrypts our credit card transactions and other secure data online. When these discoveries were made, they were profound results, but with no technological application in sight.
 Applied mathematicians often spend their time solving problems more than proving theorems. Usually, “applied mathematics” refers to the use of mathematics to gain results on problems of a mathematical nature. These problems can come from the sciences or social sciences, or from such diverse fields as business, transportation, scheduling, and communications. If you like practical applications more than theory, then applied math might be for you. For a number of resources to various websites about careers using a mathematics background, see our Career Information page.
Applied mathematicians often spend their time solving problems more than proving theorems. Usually, “applied mathematics” refers to the use of mathematics to gain results on problems of a mathematical nature. These problems can come from the sciences or social sciences, or from such diverse fields as business, transportation, scheduling, and communications. If you like practical applications more than theory, then applied math might be for you. For a number of resources to various websites about careers using a mathematics background, see our Career Information page.
Mathematics opens your mind to thinking of common things in many different ways simultaneously. For example, think of a circle and the space – called a disc – that it encompasses.
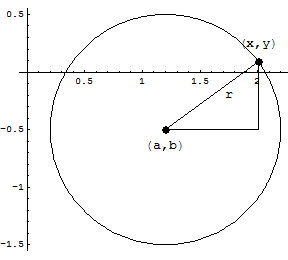
Depending on what field of mathematics you undertake, you might find useful thinking different ways about circles and discs:
- a point rotating around a center;
- the circle gives us one of the most important constants in mathematics, π (“pi”), the ratio of the circumference to the diameter;
- the arc length between two points measures the angle made between their lines intersecting with the center;
- the circle by itself and the disc have inherently different shapes (one has a “hole” and the other does not);
- a circle can be reshaped (“deformed”) into any type of closed loop that doesn’t cross itself;
- the area of the disc is the polar-coordinate integral of the circumference of the circle;
- a randomly-moving particle in the disc will hit the circular boundary before a certain time with a certain probability;
- certain types of functions on the disc take their maximum value on the circle;
- a function from the disc back to the disc has a fixed point.
Many mathematicians dealing with circles and discs use more than one of these ideas regularly, and switch between them with ease. This only scratches the surface of all the ideas and mental toys mathematicians have to play with.
There are a wide variety of programs in mathematics one may undertake in CUNY, depending on the amount of time you would like to spend in school: from associates’ degrees at CUNY’s two year community colleges, to teaching certification, bachelor’s and master’s degrees at our four-year schools, to the Ph.D. at the CUNY Graduate School and University Center. For a complete list of CUNY’s mathematics, statistics, and math education programs, visit our Programs page.
Some images courtesy Wikimedia Commons; see comments in page source for individual attributions.



